目次をご覧になりたい方はクリックしてください→
「トイレットペーパー」「2倍巻き」「大きさは何倍?」

最近、トイレットペーパー2倍巻きなるものが世の中に出回っているので、直径 (半径) は何倍になるか計算してみましょう。
もちろん紙の厚さはおなじとします。
2倍巻きならその分大きくなるはずなのに、大きさがおなじなのはおかしいですね。
つまり紙の厚さが半分ということです😄
2倍巻きなら体積が2倍になるということです。
幅はおなじなのでそのちがいは断面の円の面積を計算すれば出ます。
トイレットペーパーの長さを計算する必要もありません。
芯なし
手始めに、芯がなくて中までぎっしり紙が詰まっているものを計算してみましょう。
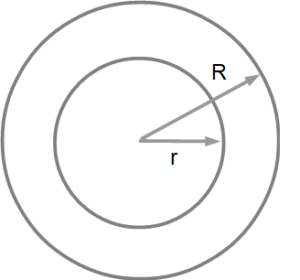
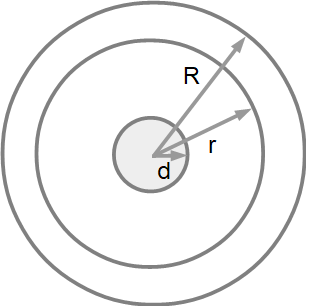
r:ふつうのトイレットペーパーの半径 [cm]
R:2倍巻きのトイレットペーパーの半径 [cm]
π:円周率
2倍巻きの半径 R は、ふつうの半径 r の「何倍」になるか計算してください。
直径は半径の2倍なので比率は変わりません。
💡 半径 R の円の面積を、半径 r の円の面積で割れば、面積の比が出ます。
これが「2」です。
最後に R は、何 r になるか計算すれば、R は r の何倍になるかわかります。
まったくおなじですが、半径 R の円の面積は、半径 r の円の面積の 2倍に等しいと考えて式をつくってもいいです。
どちらでつくってもおなじ計算結果になります。
当たりまえ。
これは「比 (率) 」なので、じっさい何cmとか、円周率はまったく関係ないのでご安心を😄
言葉で書くと複雑そうですが、計算結果は驚くほどカンタンです。
ていうかほとんど計算の必要はありません。
芯あり
つぎは芯ありだけどすこし計算が複雑になります。
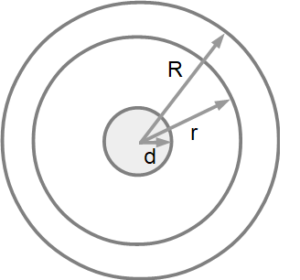
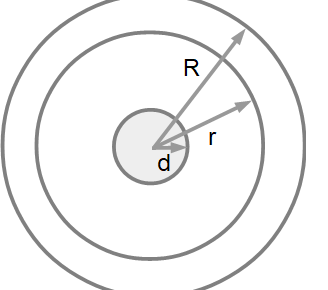
r:ふつうのトイレットペーパーの半径 [cm]
R:2倍巻きのトイレットペーパー半径 [cm]
d:芯の半径 [cm]
π:円周率
まず代数 (r, R, d, π) で計算してください。
💡 こちらは上の計算よりちょっと面倒です。
まず、半径 R の円の面積から、半径 d の円の面積 (芯の断面積) を引きます。
おなじく、半径 r の円の面積から、半径 d の円の面積を引きます。
半径 R の🍩の面積は、半径 r の🍩の面積の2倍です。
さて R を r と d で表してください。
π は消えてしまうので心配しなくていいです。
じっさい直径は何センチになる?
このままではただの代数の羅列でちがいがわからないので、
できたら具体的な数値を入れてみます。
つぎはJIS規格の標準的なサイズです。
r:6 [cm]
R:?[cm]
d:2 [cm]
JIS規格ではトイレットペーパーの直径は 12cm 以下、芯の直径は 38mm±1mm なのでここでは 4cm にしています。
半径なので半分です。
R を計算してください。
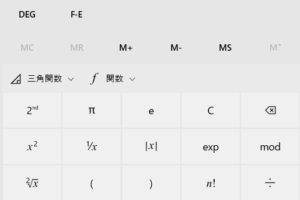
ルートが出てくるのでもちろん電卓をつかっていいですよ😄
windows付属の電卓では数値をぜんぶ計算して最後に「2√x」ボタンを押します。


答えはこちら↓