目次をご覧になりたい方はクリックしてください→
「地平線」「水平線」「どこまで見える」「ピタゴラスの定理」「近似値」

地平線 (水平線) はどこまで見えるか? ~問題
たぶん中学3年生レベルだけど、そうでない人も試してみてね。
Q. 地平線はどこまで見えるか計算してみよう!
地球の半径:R=6400km
身長 (目線の高さ) :h=150cm
見える距離:d (km) とします。
視力はかぎりなくいいものとします(^^)
地球は真ん丸とします。
途中に山や、建物、霧などの障害物はないものとします。
空気によって光が曲がることはない。直進するものとします。
距離の単位はkm。
有効数字2桁 (小数点以下1桁) で答えてください。
(つまり、小数点以下2桁目を四捨五入します)
💡 答え
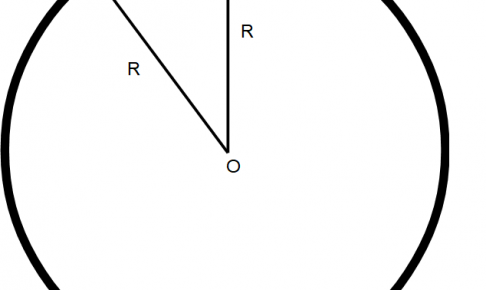
ピタゴラスの定理を使います。
はじめに単位をそろえましょう。
答えはkmなので、身長をkmに直したほうがいいですね。
$$150cm={150 \over 100}m=1.5m$$
もう1回1000で割ればkmになるけど、ここはあえて分数のままにします。
その理由はあとでわかります。
もちろん割ってしまっても全然問題ありません。
$${1.5 \over 1000}km=0.0015km$$
ただ、計算をいくらかでも楽にするテクニックです。
割ってしまうと小数点以下に「0」が並んで計算しにくいし、よく桁をまちがえます=^^=
それから、いきなり数字を入れて計算してもいいけど、これも計算を楽にするために数字の代わりにアルファベットを使います。
もちろん数字を入れて計算してもいいですよ(^^)
代数アレルギーの人ははじめから数字を入れて計算してください。
ただ、計算が大変だし、計算ミスの可能性も多くなります。
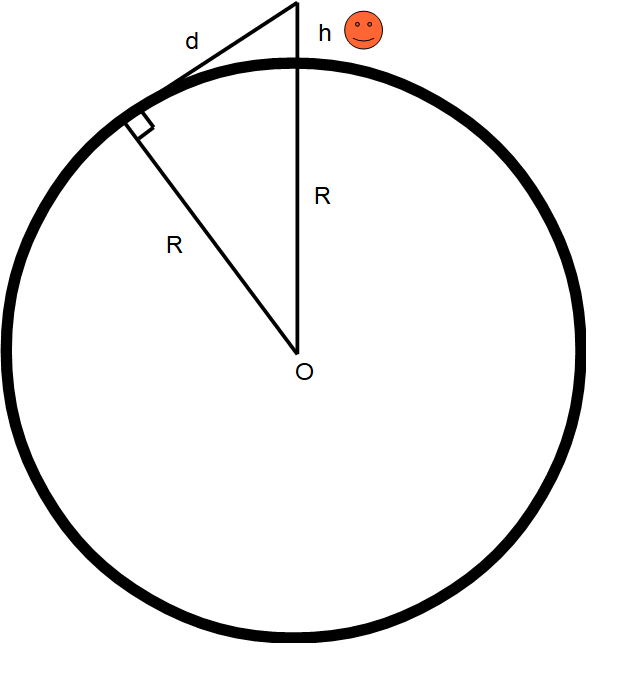
ピタゴラスの定理より
$$R^{2}+d^{2}=(R+h)^{2}$$
$$R^{2}+d^{2}=R^{2}+2Rh+h^{2}$$
$$両辺のR^{2}が消えるので$$
$$d^{2}=2Rh+h^{2}$$
2Rh≫h2なので、h2は2Rhに比べて、かぎりなく「0」に近く無視してかまいません!


$$d^{2}≒2Rh$$
$$d≒\sqrt{2Rh}$$
ここまで来たら数字を入れます。
だいぶ計算が楽になったでしょう。
$$d≒\sqrt{2 \times 6400 \times {1.5 \over 1000}}$$
これなら6400を1000で割ることができて計算の手間が省けます。
$$d≒\sqrt{2 \times 6.4 \times 1.5}$$
ここは、さらに2と1.5をかけて3にしてしまいます!
$$d≒\sqrt{3 \times 6.4}$$

$$d≒\sqrt{19.2}$$
$$d≒4.38…$$
有効数字2桁なので、頭から3桁目の小数点以下第2位を四捨五入して、
$$d≒4.4$$
地平線の見える距離
「4.4km」となりました!
1里が約4kmだから、約1里ですね。
それから、人が歩く速さは平均して4km/hなので、1時間で歩ける距離がだいたい1里なんですね。

有効数字 (ゆうこうすうじ)
この問題では、地球の半径が6400km、身長が150cmです。
数学的に、「0」は除いて、一番下の桁はその下の桁を「四捨五入」したものとして「正確でない」と判断します。
この例では、64は63.5~64.4、15は14.5~15.4と考えられ、厳密にいうと1桁しか「信用できない」数字なんです。
この場合、有効数字は3桁目を四捨五入して得られた「2桁」であるといいます。
ためしに、地球の半径を、6413とか、6394に、身長を153とか、147とかで計算してみてください。
1桁目の「4」は変わらないけど、小数点以下は「.5」になったり「.3」になったりすることがあります。
この問題では有効数字2桁で解くように指示しているので答えは「4.4」ですが、じつは2桁目は正確でないことがわかりますね。
有効数字は小数点はあってもなくても関係ありません。
あくまで「信用できる数字」が「何桁」か? です。
少ない桁の数字に合わせる
円周率は3.14159265…と続くけど、かける相手が15と2桁しかなかったら有効数字は「2桁」しかないので、円周率も3.1と2桁あれば充分です。
円周率にいくら正確な数字を持ってきても意味がないということです。





近似値 (きんじち)
上の計算で「h2」を無視してしまったけど、そのまま計算したらどうなるでしょうか?
h=0.0015 なので
h2=0.00000225 です(^^)
小数点の下に「0」が「5」コ。
最後のルートの中が 19.2+0.00000225 で、19.20000225 になります💦
$$\sqrt{19.2}≒{4.3817805}$$
$$\sqrt{19.20000225}≒{4.3817807}$$
小数点以下7桁目でやっと差が出てきます。
その差は 0.0000002 です(^^)


ほかにもこんな問題があるよ!
地球はどれくらいの速さで太陽のまわりを飛んでいるのか?~計算してみよう!
地球はどれくらいの速さで回ってるのか?~計算してみよう!
光は地球から月 (太陽) まで何秒かかるか? ~計算してみよう!
計算問題~一覧。身の回りの数学はこちら