あいてがえらんだ数字をあてる! 「九去法」

さっちゃんがえらんだ数字を、はじめからおわりまで背中を向けたままあてるよ!

え～っ!  ほんと!?

やってみよう!

用意するもの

• 紙と鉛筆だけ!  (書けるものならなんでもOK! 学校の黒板でもいいよ! )

1. 紙に自分のたんじょうびを書いてね。 (例：19851024)
2. その数字をバラバラにして、じゅんばんをいれかえて数字をつくって。「1」が2コあったら2コつかうように。 (例：51149208)
3. 大きいほうから小さいほうを引いて。 (例：51149208-19851024=31298184)
4. ひき算した答えから「0」以外の数字をひとつ数字をえらんで○をつけてね。 (例：2)
5. えらんだ数字をぬかして、のこりの数字をひとつずつゆっくり読んで。 (例：3、1、9、8、1、8、4)
6. あなたがえらんだ数字は「2」ですね!

①　はじめからおわりまで、背中を向けたままだよ! 数字を書くのも計算するのもぜんぶあいてだよ。
②　数字はたんじょうびでなくてもいいよ。家族やともだちだと、たんじょうびを知ってるから、てきとうな数をつくってもらったほうがいいかも。あまり大きな数字だと計算をまちがえてもいけないので5～10けたくらいにしておこう!
③　ひき算をまちがえたらこの手品はおわりなので、電卓をつかってもらってもいいよ!
④　あいては5.の、のこりの数字を読むときいがいは、いっさい数字をいわないよ!

どうしてわかったの!?

超能力だよ(^^)なんちゃって。それじゃあ、やりかたをおしえよう!

あなたがやること

1. あいてが読み上げる数字を、たし算します。 (例：3+1+9+8+1+8+4=34)
2. この数字 (ここでは34) よりちょっとだけ大きい、九九の9のだんの数字 (9×4=36) からこの数字 (34) をひき算します。
3. 36-34=2。2があいてがえらんだ数字です。

ちょっとわかりにくいですね。じつは、とっておきの方法があるんです。

1. 「9」はたし算しなくていいんです。「9」=「0」と思いましょう。
2. 前からじゅんにたし算していって、2けたになったら、その数字をまた分解して、たし算してしまいます。

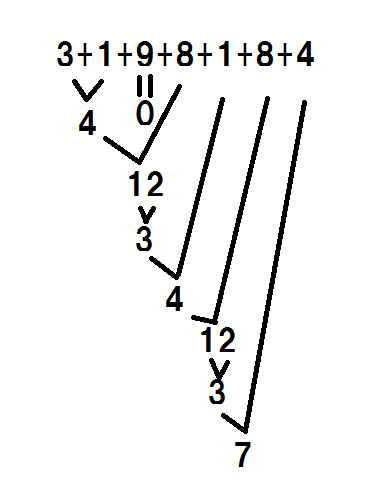
1. あいてが「3、1」といったら、あたまの中で「3+1=4」とたし算します。
2. つぎに「9」といったら、「0」と同じなのでたし算しないでほっときます。
3. つぎに「8」といったら、さっきの「4」に、この「8」をたします。「4+8=12」
4. ここですかさず「12」を「1」と「2」に分けて、「1+2=3」とたし算してしまいます。
5. 同じように、「3+1=4」
6. 「4+8=12」ここでも、「12」を「1」と「2」に分けて、「1+2=3」とします。
7. さいごに「3+4=7」になりました。
8. たし算した数字を「9」から引くとあいてがえらんだ数字になります。
9. ここでは「9-7=2」ですね!

電卓をつかってもいいけど、なにもつかわずにあたまの中で計算して、あいてのえらんだ数字を当てたほうが「すご～い! 」度があがるよ(^^)
だから、数字はひとつずつゆっくり読んでもらわないとダメなんだ。
あいてが「3」といったら、自分も「3ね」とかいいながら時間をかせぐといいよ!

ともだちには、ナイショだよ!

解説「九去法」

適当な数字をいれかえて数字をつくって、引き算すると
かならず「9の倍数」になります!

たとえば「825」という数字を考えてみましょう。

「825」をいれかえて、「258」という数字をつくったとします。

825-258=567ですね。

上でやったように、たし算していくと、
5+6=11→1+1=2
2+7=9で、「9」になりました。

どんな数字でやってもかならず「9」になります。

なんで?

825というのは、8×100+2×10+5 です。

258は、2×100+5×10+8 です。

つまり、825-258=(8×100+2×10+5)-(2×100+5×10+8) です。

これを「2」「5」「8」でまとめると、

8(100-1)-2(100-10)-5(10-1)
=8×99-2×90-5×9
=9(8×11-2×10-5)

(　)の中がなんでも「9」の倍数になりますね。

これは数学的な証明ではありません(^_^;)

ただ、桁が増えていっても、

1000-1=999
10000-1=9999
……

1000-10=990
1000-100=900
……

となるので「9」の倍数になることは間違いなさそうです。

ところで「九去法」って何?

上でやったように、数字を一桁ずつバラバラにして足していったものを「数字根」といいます。

そして、この「数字根」が「9」になると、その数字は「9」の倍数で、「9」で割りきれるのです。

足し算するときに、「9」は「0」と同じと考えて、「ほっとく」「無視する」「足さない」ということで

「九去法」といいます。

上の手品で「0」以外の数字を選んでもらうのは、「9」と「0」の区別ができないからです。

「数字根」は「9」で割ったときの「余り」を表しています。

たとえば「258」の「数字根」 (2+5+8=15→1+5=6) は「6」です。

258÷9=28あまり「6」になりますね。計算してみてください。

なぜ「数字根」が「9」 (=「0」) だと「9」で割り切れるの?

たとえば「738」という数字を考えてみましょう。

7+3+8=18→1+8=9 ですね。

738=7×100+3×10+8 です。

7×100+3×10+8
=7(99+1)+3(9+1)+8
=7×99+7+3×9+3+8
=(7×99+3×9)+(7+3+8)
=9(7×11+3)+(7+3+8)

前の方の「9」がついてる数字は「9」で割り切れるので、問題はうしろの「一桁の数字の和」 (ここでは、7+3+8) です。

これが、「9」で割ったときの、「余り」で、これが「9」の倍数なら「9」で割りきれるわけですね。

ちなみに数学的な証明ではありません(^_^;)

「数字根」「何で割りきれるか」いろいろ

ほかにも何の倍数か (何で割りきれるか) わかるものがあります。

数字根が「3」の倍数なら「3」で割りきれる。

たとえば「258」なら 2+5+8=15→1+5=6 なので「3」で割りきれます。

「259」なら、2+5+9=16→1+6=7 なので「3」で割ると、「1」余ります。

数字根が「3」の倍数で、「偶数」なら「6」で割りきれる。

2×3=6 なのでこうなりますね。

下3桁が「4」で割りきれれば、その数字は「4」で割りきれる。

「100」は「4」で割りきれるので。

下4桁が「8」で割りきれれば、その数字は「8」で割りきれる。

「1000」は「8」で割りきれるので。

1の位が、「0」か「5」なら「5」で割りきれる。

九九の「5」の段、いってみましょう。

九九の「9」の段。一の位と、十の位を足すと「9」になる。

9、18、27…72、81。

3桁の同じ数のくりかえしは「7」で割りきれる。

「358358」のような数字。

358358=358×1001

1001=7×11×13

つまり、「11」「13」でも割りきれます。
あまり使うことないと思うけど(^^)

魔法の数字 ～『142857』

「ほかにもこんなのあるよ」っていうのがあったらおしえてね(^^)

たのしい算数・みのまわりの数学 ～ 一覧はこちら

計算問題 ～ 一覧。みのまわりの算数・数学

ほかにもこんな手品があるよ!

子どもでもできる! おもしろ手品

相手がえらんだカード (トランプ) を当てる! (カードマジック15枚)

コインの瞬間移動! 4枚のコインがつぎつぎに1カ所に集まる!

「魔法陣」をつくろう!

相手が選んだ4つの数字の合計を予言する!

見てね!

おじさんオススメの記事

飛行機はなぜ飛ぶか? ～「迎え角」と「コアンダ効果」

注目の記事

「右・左・右」はまちがい! 人は左から来た車に はねられる! 当たり前です!

話題の記事

シャンプーが水っぽくなるのはなぜ? (図解)

人気の記事

相手がえらんだカード (トランプ) を当てる! (カードマジック15枚)