目次をご覧になりたい方はクリックしてください→
「円周率 (えんしゅうりつ) 」「円の面積」



円周率をもとめてみよう!
用意するもの
-
丸いもの (コップ、なべなど)
-
やわらかいメジャー (なければ、ヒモと、ものさしでもできるよ! )
やってみよう!
- メジャーで、コップのまわりの長さ (円周) をはかります。
- ものさしで、コップの直径をはかります。
これだけです! 簡単。すぐできますね。
⏰ 目安時間。5分。 (準備の時間はふくまれません)

メジャーで、コップのまわりの長さをはかります。メジャーが見当たらなかったので、ヒモを巻きました。

ものさしで、コップの直径をはかります。

ヒモをまいた時は、グルッと一周したところをしっかり持って、ものさしで長さを測ればいいです!
円周をはかるときは、ヒモをたるませないように、でもひっぱりすぎて伸ばさないように。
たるませると長めに、ひっぱると短くなってしまうよ。
厚みがあるものは外側をはかってね。 (外径)
なべでも同じことをやってみましょう。


円周率をもとめよう!
円周を直径で割るだけです。ちなみに、今回おじさんがはかった結果はこうなりました。
| 円周 | 直径 | 円周率 (円周÷直径) | |
| コップ | 262mm | 81mm | 3.23 |
| なべ | 638mm | 206mm | 3.10 |
3.14に当たらずとも遠からずですね。
そもそも円周率ってなに?
直径に対して、円周のわりあいがどれくらいかをあらわします。
「比」とか「率」とか、合わせて「比率」とかいいます。
直径を「1」とした場合、円周は「3.14」ということです。
円周は直径の「3.14倍」と言いかえてもいいでしょう。
たとえば直径が1mの木なら、円周は3.14mということです。
直径に「3.14」をかけると、円周がもとめられます。

比率なので、円の大きさに関係なく、一定の数であること!
「無次元数」
ちょっとむずかしい話をします。わからなくても大丈夫ですよ!
円周率は、長さ÷長さ。ここでは[mm]÷[mm]と、同じもので割っているので、単位がありません。
こういう数字を「無次元数」とよびます。
リンゴが1個とか、えんぴつが3本など、ものの数も「無次元数」です。
えっ? 「個」とか「本」って単位じゃないの?
日本語には、「個」とか「本」とかつくのでまぎらわしいけどこれは単位ではないんです。
英語にはこういうことばはなくて、リンゴでも、えんぴつでも、1、2、3としか数えません。
日本語でも「ひとつ」「ふたつ」「みっつ」と数えますね。
ひとつ、ふたつと数えられるものは無次元数です。
円の面積をもとめてみよう!
用意するもの
-
紙 (すこし厚めの紙のほうがあとで組みあわせやすいです)
-
はさみ
-
コンパス
-
ものさし
⏰ 目安時間。15分。
やってみよう!

紙にコンパスで円をかきます。

円を半分にわけます。
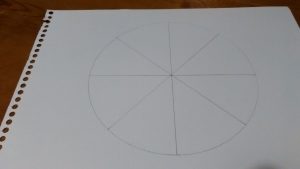
また半分にして1/4に。また半分にして1/8にわけます。ケーキをわける感じでね!

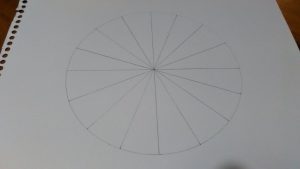
また半分にして1/16にします。

ここでは説明のために、あとでわかりやすいように上と下を色分けします。しなくてもいいですよ。

円をくり抜きます。

半分に切ります。

ケーキを切るように線を入れたところを切っていきます。外側の丸いところだけは切らずにつなげておいてください。もし、切れてしまっても大丈夫ですよ。下の写真のように組みあわせればいいです。

切れ目を広げます。 サメの歯みたいになりましたね(^^)

上下の歯をかみ合わせます。円が平行四辺形になりました。平行四辺形の面積は「横×高さ」でしたね。
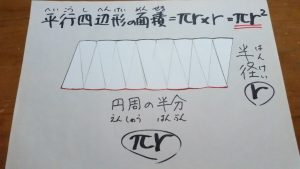
横は「円周の半分」。高さは「半径」です。
円を切りひらいて組みあわせると、平行四辺形になりました。
文字だとわかりにくいので、上の最後の写真を見ながら読んでください。
平行四辺形の面積は=「横」×「高さ」
平行四辺形の面積は=「横」×「高さ」
① まず「横」の長さを見てみましょう。
横は「円周の半分」ですね。
「円周=直径×3.14」なのでその半分。
「直径×3.14÷2」です。
せっかく、直径で説明してきたけど、円は「半径」で表されることが多いので
「半径」にかえます。
つごうのいいことに「直径÷2=半径」なので
「直径×3.14÷2=半径×3.14」です。
② つぎに「高さ」を見てみましょう。
ズバリ「高さ」=「半径」ではないですか!
③ あとは「横」と「高さ」をかけるだけ。
「横」×「高さ」=「半径×3.14」×「半径」
したがって円の面積は
「半径×半径×3.14」
「半径×半径×3.14」
でもとめられることがわかりました!
πはギリシャ文字でパイと読み、円周率 (3.14) をあらわします。
数学では、半径を「r」、円周率を「π」であらわします。
「半径×半径×3.14」を「π」と「r」に書きかえると「πr 2 」になります。
「r 2 」は「r」を2つかけるという意味です。
円周は「2πr」です。
ちなみに円周を「積分」すると、「円の面積」に。
「円の面積」を「微分」すると、「円周」になります。
ちょっとむずかしかったかな?

紙にケーキの絵を書いて切ってみてね!
他のもとめ方
多角形で円をはさむ
① 正方形ではさむ
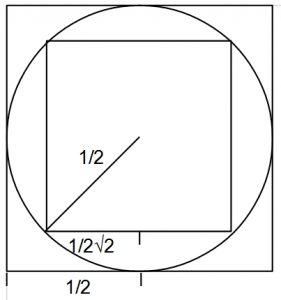
こうすると円周は内側の正方形の外周より大きく、
外側の正方形の外周より小さいことがわかります。
円の直径を「1」とすると
内接する正方形の外周は 4/√2≒2.8
外接する正方形の外周は 4なので
2.8<円周<4
であることがわかります。
まだまだ大雑把すぎますね。
なので次は六角形でやってみましょう。
② 六角形ではさむ
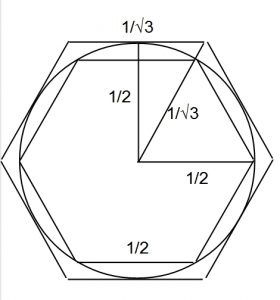
上の正方形と同じように、円周は内側の六角形の外周より大きく、
外側の六角形の外周より小さいことがわかります。
円の直径を「1」とすると
内接する六角形の外周は 1/2×6=3
外接する六角形の外周は (1/√3)×6≒3.46なので
3<円周<3.46
だいぶ3.14に近づいてきました!
こうして多角形を増やしていくと、限りなく円に近づいていきます。
ここから先は三角関数を使わないと解けません。
私は数学に自信がある! というかたは挑戦してみてください。
こぼれ話
「円周率は3」
ゆとり世代がこう習ったという噂が広がり定着しましたが、
これはある学習塾が宣伝のために作り上げた話のようです。
「小数点のかけ算を習う前に、円の面積を計算する必要があるときには
3をつかってもいい。」
ということが学習指導要領に書かれていて
それをネタに学習塾が保護者の不安をあおって塾に通わせるという算段だったようです。
実際に「円周率は3」になったわけではないようです。
「わたしはほんとに円周率は3と習いました! 」
という方がいらっしゃったらコメント欄にお書きくださいm(_ _)m
円周率は3で何も問題はない!
みなさんは「3.14」が円周率だという固定観念があると思いますが
そもそも小数点以下2桁でなければならない理由も根拠もありません。
これを言ったらおしまいですが、学校を卒業して、
いや、在学中でも授業以外で、学校の外で、日常生活でも、会社でも
3.14を使ったことが一度でもありますか?
ないですよね。
かりに木の幹周りを計算してみましょう。
直径1mの木の円周は、円周率3なら3m。
円周率3.14なら3m14cm。
14cmしか違いません。
そもそも木の直径って、切り倒さないとはかれませんね(^^)
もし研究者とか、機械系の仕事で使うことになればそのときにおぼえればいいし
そのときにいくらでも調べられるし、そういった専門の仕事の場合、
反対に、3.14じゃ大雑把すぎて話にならないんです。
金属加工などは精度が求められるので、3.1415926まで使うそうです。
たとえば直径10mの円盤を作るときに、3.14で計算したら
円周が31mと40cmで誤差が1.6cmもできてしまうからです。
日常生活ではまったく問題ないレベルですが、金属と金属の鉄骨を合わせてビルを建てるときなどは、1.6cm隙間が空いたら大変なことになります。
ボルト穴も合わず組み立てることができません。
有効数字
なんでもかんでも小数点以下の桁数が多ければいいというものではありません。
上に書いたように何に使うかによってどれくらいの精度が必要かということが1つあります。
2つめに、数字にもかける相手との相性があるのです。
こっちががんばって3.14159265を持ってきても、かける相手がたとえば2.3と2桁だったら、
答えが小数点以下10桁あっても、2桁までしか信頼性がないんです。
デートで目一杯ドレスアップしてきたのに、あいてがジャージでやってきたら、
食事をする場所がレストランではなく、ファーストフードになってしまうようなもんですね=^^=
レベルの低いほうに合わせなければならないんです。
数学的な説明は省きますが、かけ算をした場合、
少ない桁数の数の桁までしか信頼性がないんです。
小数点以下何桁かではなく、全体で何桁かです。
2.3だったら2桁と数えます。
この場合、円周率は3.1までしか意味がありません。
これを「有効数字」といいます。
円周率は「無理数」でどこまでいっても割りきれない!
厳密には、整数の分数で表せない数ですが、ここでは説明しません。
気になった方は、検索してみてください=^^=
円周率のおぼえ方
みなさんの生活にはなんの役にも立たないけど、ゴロ合わせでこんなものを作った人がいます。
おぼえたら、人に「へえ~すごいね~」くらいは言われるかもしれません(^^)
産医師異国に向こう 産後薬なく 産に 産婆 四郎二郎 死産
産婆さんに泣く ご礼には 早 (はよ) 行くな
3.141592653589793238462643383279502884197
これで小数点以下39桁までおぼえられます。
英語には、Yes, I have a number! (単語の文字数で3.1416) なんてのがあるらしいです。
ん? どっかで聞いたような…
くりかえしますが、おぼえてもなんの役にも立ちません(^^)
英語では円周率に相当することばがない?
the ratio of the circumference of a circle to its diameter
「直径に対する円の円周の率」
というらしいです。長いですね。そのままじゃないですか(^^)
なので普通は単に”Pi” (パイ) といいます。
大工の指金 (さしがね)
大工さんの使う指金は、裏返すと、角目 (√2倍の目盛り) と、丸目 (1/3.14倍の目盛り) がついています。

角目 (かくめ)。 √2倍になっているので、裏返しにして角目で円の直径を測ると、内接する正方形の一辺の長さが計算しなくてもわかります。丸太から角材を取りたいときに便利です。ちなみに単位は尺貫法で1分≒1/33mです。

丸目。1/3.14 (円周率の逆数) で目盛りがふってあるので、丸目で直径を測ると、円周の長さが計算しなくても出ます。こちらも単位は尺貫法なのでmmに似てるけど、ちがいます。
つかったもの





円周率を使う問題はこちら
地球はどれくらいの速さで太陽のまわりを飛んでいるのか?~計算してみよう!
地球はどれくらいの速さで回ってるのか?~計算してみよう!