目次をご覧になりたい方はクリックしてください→
「月」「5円玉」「穴」「視角」「日食」
5円玉の穴 vs 月 ~ どっちが大きい?


5円玉の穴から月が見えるか?
月のほうが大きいのはみんな知っています。
でも、夜空に浮かぶ月の直径が3500kmもあるようには見えません。
それは、38万キロというとても遠いところにあるからです。
それでも5円玉よりは大きく見えますね。
5円玉を親指と人差指で持って、腕をのばして、その穴から月が見えると思いますか?
5円玉を目に近づけてのぞけば見えます。
問題は腕をのばして見えるかどうかです。


やってみよう!
用意するもの
5円玉
あとは月がのぼるのを待つだけ!
- 5円玉を親指と人差指で持って腕をのばします。
- その穴から月を見ます。



ぜひ、じっさいに見てください。
お金も時間もかかりません。
あっ、5円だけかかります😄
でも、手元にもどってきます!
この記事だけ見て「ふ~ん。そうなんだ」と納得しないで、「そんなわけないやろ! 」とツッコみながら見てください。
論より証拠。百聞は一見にしかずです✌
視角
人は離れた物のじっさいの大きさを知ることはできません。
目に入ってきたときの「視角 (角度) 」しかわからないのです。
じっさいの大きさではなく「視角 (角度) 」で大小を判断している
視角がおなじだと、おなじ大きさに見えます。
視角とは?
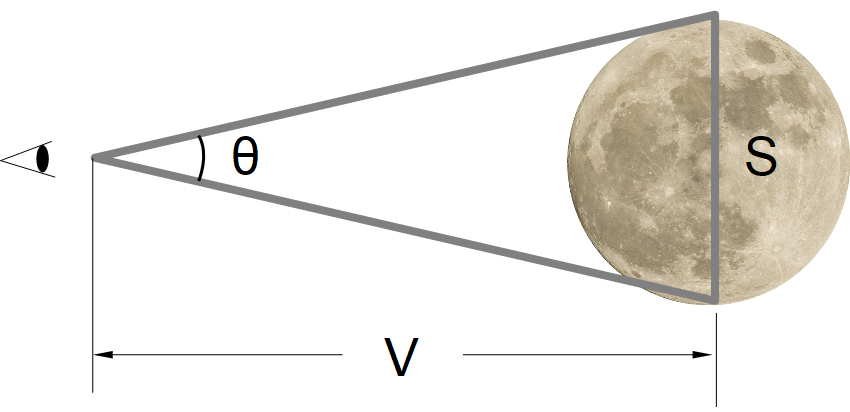
S:サイズ (大きさ、高さ、直径など)
V : 距離
θ:視角
二等辺三角形を半分に割って、2つの直角三角形にしてから計算するのはめんどうなので、近似式 (近似値) をつかいます。
近似式
視角が10度より小さいときは直角三角形とほぼ同じ
大きく見える月も、じっさいの視角は0.5°くらいしかありません。
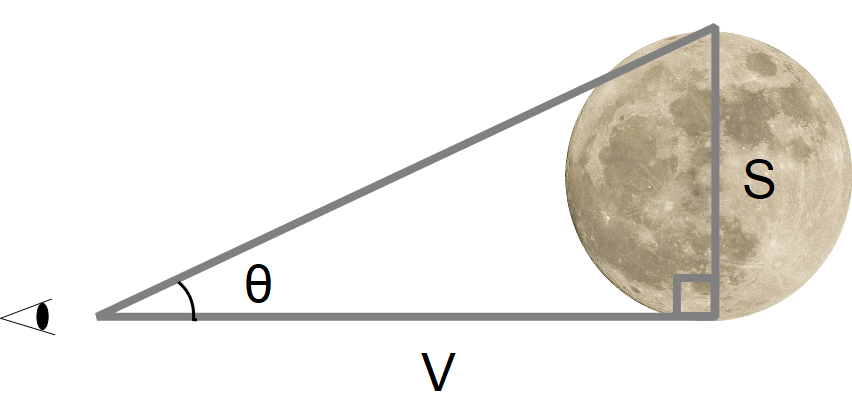
tangent (タンジェント) と arctangent (アークタンジェント)
すると次のような式が導かれ、視角θをもとめることができます。
$$ \tan \theta = \frac{ S }{ V }$$
$$ \theta = \arctan \frac{ S }{ V }$$
tan (tangent) は高さ ÷ 底辺
arctan (arctangent) はtangent から角度をもとめるものです。


では、それぞれの視角を見ていきましょう。
月の視角
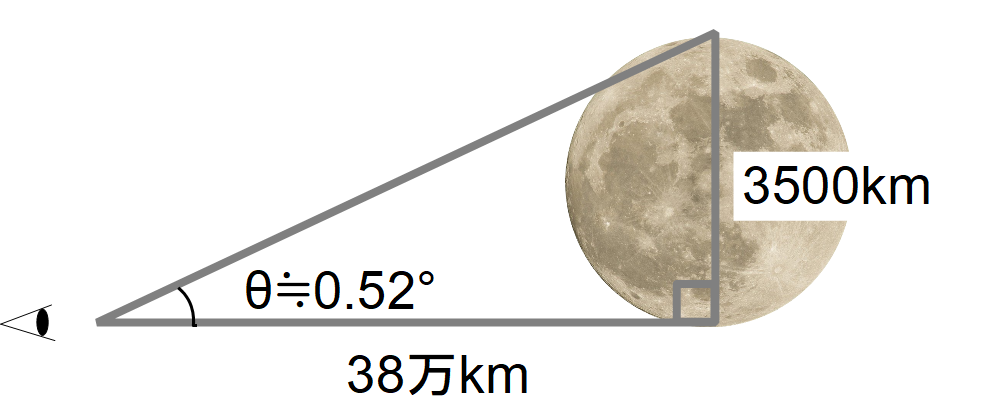
月
直径:3500km
距離:380000km
$$ \tan \theta = \frac{ 3500 }{ 380000 }≒ 0.0090 $$
$$ \theta = \arctan 0.0090 ≒ 0.52^{ \circ }$$
5円玉の穴の視角
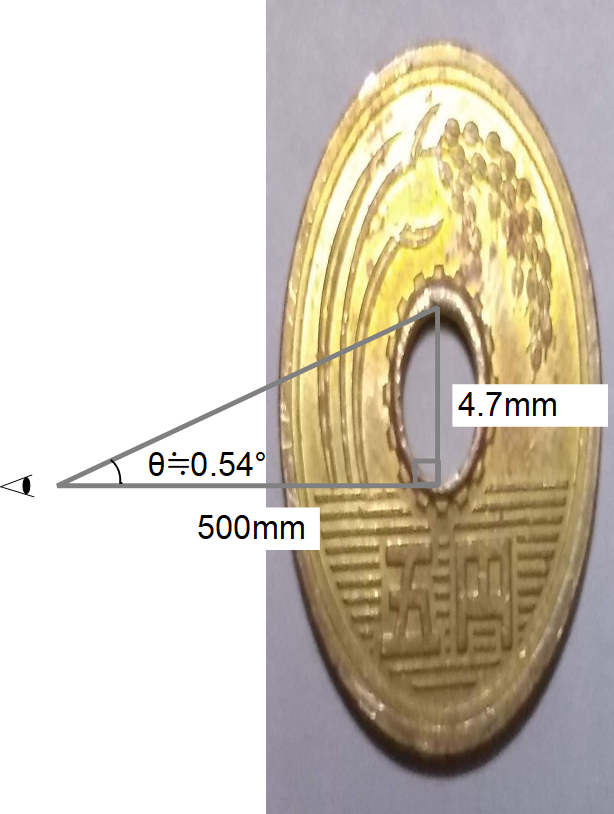

5円玉の穴
直径:4.7mm
距離:500mm
(手の長さではなく、目から5円玉までの距離です。手が極端に長い人は見えないかも💦)
$$ \tan \theta = \frac{ 4.7 }{ 500 }≒ 0.0094 $$
$$ \theta = \arctan 0.0094 ≒ 0.54^{ \circ }$$


太陽の視角
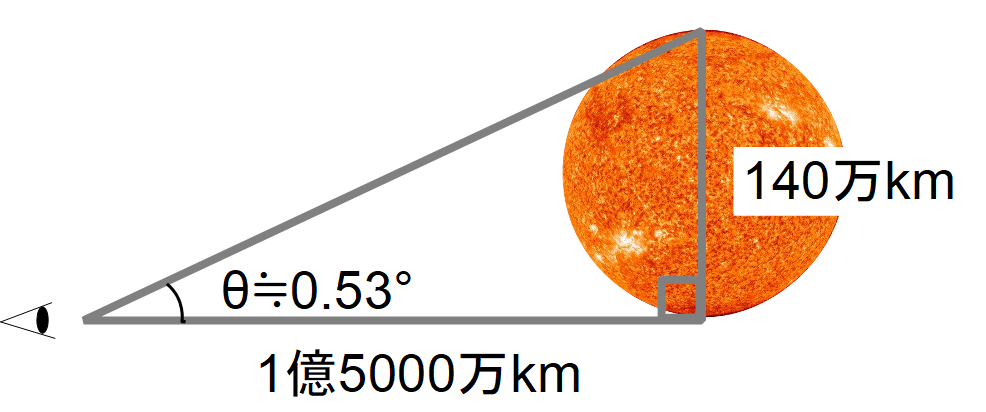
太陽
直径:140万km
距離:1億5000万km
$$ \tan \theta = \frac{ 140 }{ 15000 }≒ 0.0093 $$
$$ \theta = \arctan 0.0093 ≒ 0.53^{ \circ }$$




月はいつかいなくなる! そして地球は止まる! ~永年減速

ちなみに50円玉は
直径:3.5mm
距離:500mm
5円玉より穴が小さいんですね。
$$ \tan \theta = \frac{ 3.5 }{ 500 }≒ 0.0070 $$
$$ \theta = \arctan 0.0070 ≒ 0.40^{ \circ }$$
日食
皆既日食と金環日食

上の計算だと、太陽の視角のほうが月よりすこしだけ大きいのでかならず太陽がはみ出て金環日食になるはずです。
なぜ皆既日食 (完全に隠れる) が起こるのでしょうか?
地球も月も楕円軌道
地球は太陽のまわりを回り、月は地球のまわりを回っています。
でも、正円 (まんまる) ではなく、すこし楕円 (たまご型) をしているのです。
だから、地球と太陽、地球と月の距離はいつも変化しています。
遠日点と近地点
地球と太陽の距離が離れる (遠日点) と太陽は小さく、地球と月の距離が近づく (近地点) と月は大きく見えます。
このときに日食が起こると皆既日食になります。
ちなみに北半球では真夏に遠日点を通るので、太陽は地球から離れて小さくなっています。


遠近法
この言葉はだれでも聞いたことがあり、経験的に知っていますね。
「遠いと小さく、近いと大きく見える」
車が近づいてくるとだんだん大きくなり、離れていくとだんだん小さくなるけど、車が大きくなったり、小さくなったりしているのではなく、近づいたり、離れたりしているということを知っています。
このとき変わるのは、車の大きさではなく、「視角」です。
心理的、経験的、知識的に大きさを判断している
経験的に大きさを知っている
遠くに離れれば小さく見えることはわかっているけど、経験的にバイクよりトラックのほうが大きいことを知っています。
だから、遠くに小さく見えてもトラックは大きいと判断します。
おなじように月は空に浮かんでいる星だ、大きいものだという知識から、5円玉の穴よりはるかに大きく見えます (感じます) 。
でも、じっさいに網膜に映った大きさはほぼ同じなんです。
錯覚
でも、同じ距離にいても、トラックは大きく見えるので近くに、バイクは小さく見えるので遠くにいると錯覚してしまいがちです。
車の運転をするときや、道路をわたるときは気をつけましょうね✌
バイクはあなたが思ったより近くにいます。
光は地球から月 (太陽) まで何秒かかる? ~計算してみよう!
月はいつかいなくなる! そして地球は止まる! ~永年減速
太陽と地球と月の大きさと距離 ~ ほんとはこんな感じ
かぐや姫は托卵?なぜわざわざ地球に?
月の謎 ~ 月にまつわる話
計算問題 ~ 一覧。みのまわりの算数・数学








いつも面白い切り口の記事、よく気が付きますね
海野さん。
ありがとうございます。
5円玉と月は、いまから40年以上前、どこかで読みました。
覚えていたのはじっさいにやってみたからです!