目次をご覧になりたい方はクリックしてください→
「鉛筆」「芯」「使用率」「計算」
鉛筆の芯。どれだけ使ってる?
鉛筆ってすりへったら削って使うけど、じっさいはどれだけ使ってるんでしょう?

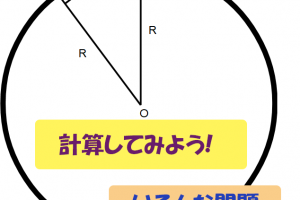
問題はこちら。鉛筆の芯。どれだけ使ってる? ~計算してみよう!
計算してみよう!
- 鉛筆 (芯) の長さ。17cm
- 芯の太さ。2mm
- 1/4すりへったら、削る。
- 残りが7cmまで使ったら終わりにします。つまり、じっさいに使うのは10cm
- 円周率は3.14とします。
何%使ってるか?
- 元の芯の体積を求めます。
- じっさいに使ってる部分の体積を求めます。
- ② ÷ ① × 100 で「%」を求めます。 (小数点以下四捨五入)
- じっさいに使う長さを、最初の長さで割ります。
💡 ヒント
- 円錐の体積の求めかたが必要です!
- 割合 (%) を求めるだけなら、じつは長さと太さは関係ありません!
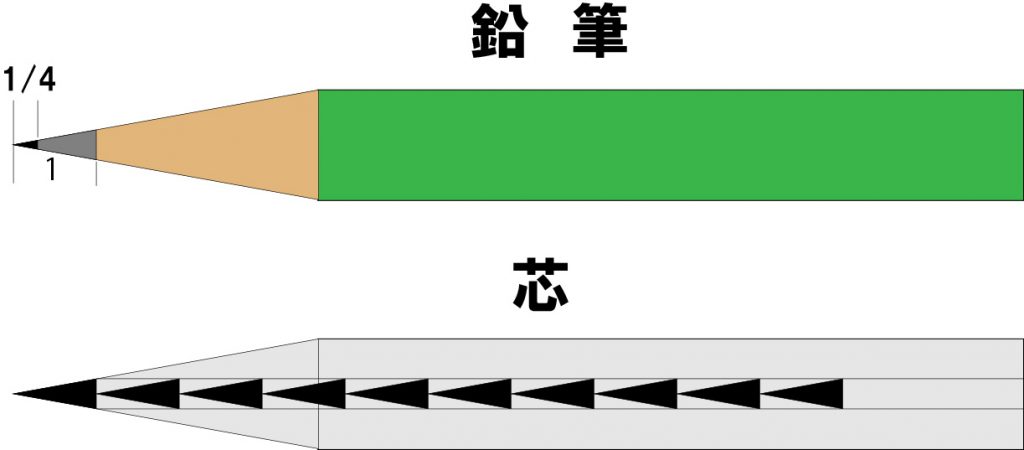
※ 芯の絵はイメージで正確なものではありません。
答え
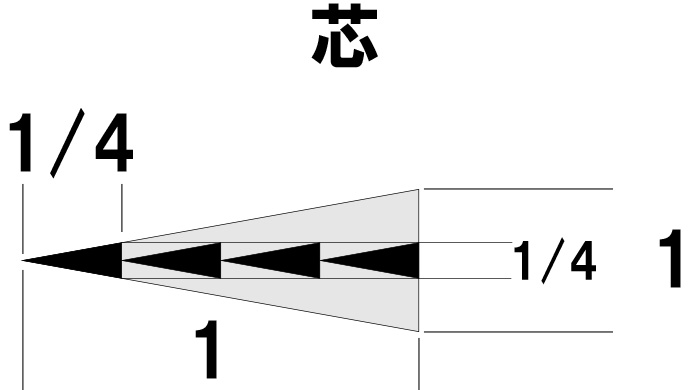
割合 (%) をもとめる
まず1、2は飛ばして、3の割合だけ求めてみましょう。
なぜなら、このほうが簡単だからです。
円錐の体積
円錐の体積 = 円柱の体積 ÷ 3
上のさし絵は鉛筆の芯だけを書いてます。
灰色の部分も芯です。
もし鉛筆を削らないですべて使えば、灰色の円柱の部分をすべて使うことになります。
上の図ではもう削った絵を書いているけど、削る前は「円柱」です。
「1」「1/4 (4分の1) 」と書いてあるのは、あくまで長さの比で、じっさいの寸法ではありません。
相似の三角形なので、長さが1/4なら、太さ (直径、半径) も1/4になります。
長さ (円錐の高さ) を「h」
太さ (半径) を「r」
円周率を「π」
円柱の体積 (もともとの鉛筆の芯) を「V」
大きな円錐の体積を「V1」
小さな円錐4コ分の体積を「V2」とします。
円柱の体積Vは、「円の底面積×高さ」なので
$$V={ hπr^{2}}$$
大きな円錐の体積V1は、「円柱の体積 ÷ 3」なので
$$V_1={ hπr^{2} \over 3}$$
さらに「1」の長さの円錐のところを見ると、長さ「1/4」、半径「1/4」の円錐が4コになっているのがわかります。
なので、ちっちゃい円錐4コ分の体積V2は、
$$V_2={ 4hπr^{2} \over 4\times3\times4^{2}}$$
長さのほうは、1/4のものが4コあるので、通分して「1」になります。
$$V_2={ hπr^{2} \over3\times4^{2}}$$
もう見てわかると思うけど、ちっちゃい円錐の体積は、元の鉛筆の芯 (円柱) に対して
$$V_2 \div V $$
つまり
$$ { hπr^{2} \over3\times4^{2}} \div {hπr^{2} } $$
$${hπr^{2}} は消えてしまうので、残りは$$
$$ { 1 \over3\times4^{2}} だけ! $$


無次元数 (むじげんすう)
「体積」÷「体積」のような「比」は「単位」がなくなってしまいます。
これを「無次元数」といいます。
無次元数についてはこちら。円周率は3?
分母を計算するとこうなります。
$$ { 1 \over48 } ≒ { 1 \over50 } = 0.02$$
「2%」しか使ってないことになります!





さらに
じっさいには鉛筆を端から端まで使うことはできません。
17cmの鉛筆を10cmまで使って、残りの7cmは捨てるとすると、
使うのは
$$\frac{10}{17}≒{0.6} (60%) $$
最終的には、0.02 × 0.6 = 0.012
「1%」しか使ってません=^^=
これは長さにすると、
17cm × 0.01 ≒ 0.17 cm = 2 mm になります!
なので、おじさんは「鉛筆サック (ホルダー) 」を使ってここまで使い切ります。








計算問題~一覧。身の回りの数学はこちら
おじさんオススメの記事
注目の記事
話題の記事
人気の記事