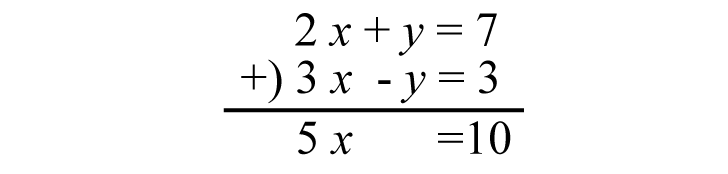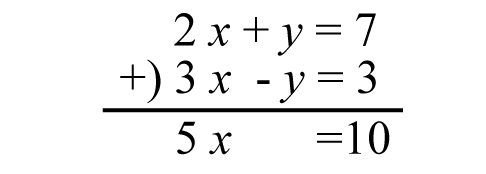目次をご覧になりたい方はクリックしてください→
「連立方程式」「シーソー」「等号」
連立方程式もしょせん「 = (等号) 」で結ばれた「シーソー」
たとえばこんな連立方程式があります。
$$\begin{eqnarray} \left\{ \begin{array}{l} 2x + y = 7 \\ 3x – y = 3\end{array} \right. \end{eqnarray}$$
一般的な解きかたは、
片方を「 x 」か「 y 」の式にして、
もう一つの式に「代入する」というやり方です。
もちろんこれでいいです。
ただ、おじさんは楽したいので、条件さえよければ
「連立方程式」ごと「足し算」「引き算」
してしまいます。
このほうが計算が楽だし、
計算が「楽」ということは、
「まちがいも少ない」ということなんです。
計算が複雑になればなるほど、とうぜんまちがいも多くなります。
連立方程式ごと足し算、引き算
例をよく見ると、上の式では「 + y 」、
下の式では「 – y 」ということに注目します。
この場合、上下で足し算をすると
「 y が消えてしまう! 」ではありませんか!
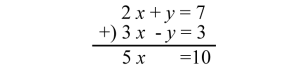
$$ x = 10 \div 5 $$
$$ ∴ x = 2 $$
あとは x の値 ( 2 ) をどちらかの式に入れてやれば、y が求められます。
どちらでもいいけど、この場合もできるだけ計算を楽に、まちがいを少なくするには、
y の符号が + で、
x にかかってる数字も小さい上の式のほうがいいですね。
= (等号) は「シーソー」
等号は「シーソー」または「天秤」のようなもので、
左右に「同じ重さのものが乗ってる」
と考えてください。
たとえば上の式だと、
左は 2x + y、右は 7 と
姿形はぜんぜんちがうけど、
「重さ」はまったく同じです。
単位が kg なら、
2x + y も 7 kg ということです。
下の式なら、
3x – y も 3 kg ということです。
だから、それぞれ上下に足しても、引いても、シーソー (等号) のバランスはくずれないんです。
シーソー (等号) についてはこちらに書いてます。
移項~なんで「+ -」「× ÷」が逆になるの?
つぎの連立方程式の場合は引き算します
$$\begin{eqnarray} \left\{ \begin{array}{l} 2x + y = 7 \\ 2x – 3y = -5\end{array} \right. \end{eqnarray}$$
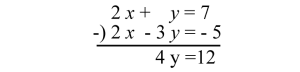
$$ y = 12 \div 4 $$
$$ ∴ y = 3 $$


二元一次方程式
なんて書くと数学に恐れをなしてしまうけど、
「元」は x や y みたいに
「わからないもの (代数) 」
のことで、
わからないものが「2コ」という意味です。
もう1コ、z が加わると「3元」になります。
「次」は、
この「わからないもの」どうしが
「何回かけられているか」
ということで、x、y にかけられている数字の2とか、3は関係ありません。
x2 (= x × x) , y2 ( = y × y ) のように
代数が「2回」かけられていると、
「2次」といいます。
「2乗」ということですね。
x3 と「3乗」になると、
「3次」になります。
「わからないものが2コ、3乗方程式」とか言えばわかりやすいかな(^^)
代数
x とか、y とか、これもむずかしさを、かもし出してるけど、西洋の人が数学を考えたのでしかたないですね(^^)
別に、x や y である必要はまったくなくて、日本だったら「あ」や「い」でもよかったんです。
こんな具合ですね。
つぎの連立方程式から、
「あ」と「い」を求めなさい。
$$\begin{eqnarray} \left\{ \begin{array}{l} 2あ + い = 7 \\ 3あ - い = 3\end{array} \right. \end{eqnarray}$$
動物や果物でも。○△□でも。
つぎの連立方程式から
🐰と🍎を求めなさい。
2🐰 + 🍎 = 7
3🐰 – 🍎 = 3



たのしい算数・みのまわりの数学 ~ 一覧

おじさんオススメの記事
注目の記事
話題の記事
人気の記事