目次をご覧になりたい方はクリックしてください→
「トイレットペーパー」「2倍巻き」「大きさは何倍?」

トイレットペーパー2倍巻きは直径何倍になる?~ 問題

最近、トイレットペーパー2倍巻きなるものが世の中に出回っているので、直径 (半径) は何倍になるか計算してみましょう。
もちろん紙の厚さはおなじとします。
2倍巻きならその分大きくなるはずなのに、大きさがおなじなのはおかしいですね。
つまり紙の厚さが半分ということです😄
2倍巻きなら体積が2倍になるということです。
幅はおなじなのでそのちがいは断面の円の面積を計算すれば出ます。
トイレットペーパーの長さを計算する必要もありません。
芯なし
手始めに、芯がなくて中までぎっしり紙が詰まっているものを計算してみましょう。
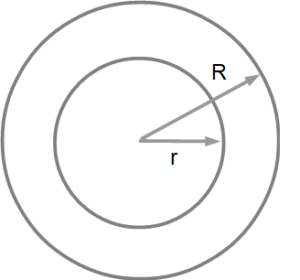
r:ふつうのトイレットペーパーの半径 [cm]
R:2倍巻きのトイレットペーパーの半径 [cm]
π:円周率
答え
2倍巻きの半径 R は、ふつうサイズの半径 r の「何倍」になるか計算してみましょう。
直径は半径の2倍なので比率は変わりません。
$$ 円の面積は \pi r^2 ですね。$$
$$ 2倍巻きの面積:\pi R^2 $$
$$ ふつうサイズの面積:\pi r^2 $$
なので
$$ \frac{\pi R^2}{\pi r^2}=2 $$
分子、分母に π があるのでいきなり消えます。
さよなら👋
$$ \frac{R^2}{r^2}=2 $$
$$ R^2=2 r^2 $$
$$ R=\sqrt{2 r^2} $$
$$ ∴ R=\sqrt{2} \ r $$
ということで、2倍巻きの半径はふつうサイズの√2倍。
約 1.4 倍になりました。
もちろん直径の比率もおなじです。
√2
いちおう順を追って計算しましたが、面積というのは2次元で、縦 [m] × 横 [m] で [m2] になります。
この単位の [m] の右肩に小さい「2」が乗っているのは伊達ではありません。
これは縦の長さ (1次元) と横の長さ (1次元) をかけて2次元になっているということを表しています。
だから正方形でも1辺の長さが √2倍になると、面積はその2乗、つまり 2倍になります。
1辺の長さが2倍になれば面積は4倍です。
円の面積も円周率など関係なく、直径 (半径) が √2倍になれば面積は 2倍。
直径が 2倍になれば面積は4倍になります。
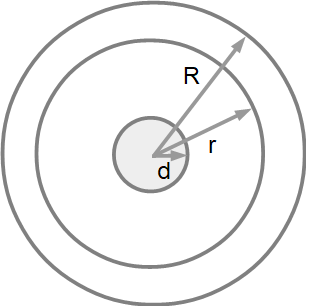
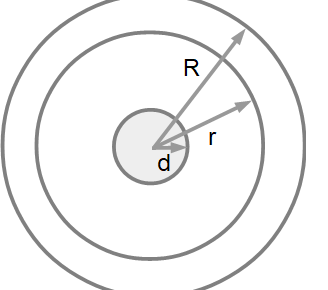
芯あり
つぎは芯ありだけどすこし計算が複雑になります。
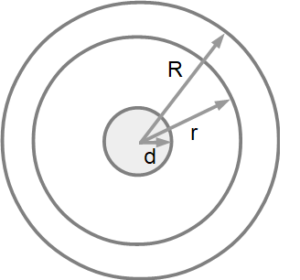
r:ふつうのトイレットペーパーの半径 [cm]
R:2倍巻きのトイレットペーパー半径 [cm]
d:芯の半径 [cm]
π:円周率
まず代数 (r, R, d, π) で計算してみましょう。
2倍巻きの面積-芯の面積 🍩:
$$ \pi R^2 – \pi d^2 = \pi (R^2 – d^2) $$
ふつうサイズの面積-芯の面積 🍩:
$$ \pi r^2 – \pi d^2 = \pi (r^2 – d^2) $$
2倍巻きの🍩のほうが面積が2倍になるので
$$ \frac{\pi (R^2 – d^2)}{\pi (r^2 – d^2)}=2 $$
$$ またもや \pi は消えるので $$
$$ \frac{R^2 – d^2}{r^2 – d^2}=2 $$
$$ R^2 – d^2=2(r^2 – d^2) $$
$$ R^2=2(r^2 – d^2) + d^2 $$
$$ R^2=2r^2 – 2d^2 + d^2 $$
$$ R^2=2r^2 – d^2 $$
$$ ∴ R=\sqrt{2r^2 – d^2} $$
こんどはちょっと複雑な式になりました🤔
じっさい直径は何センチになる?
このままではただの代数の羅列でちがいがわからないので、
具体的な数値を入れてみましょう。
つぎはJIS規格の標準的なサイズです。
r:6 [cm]
R:?[cm]
d:2 [cm]
JIS規格ではトイレットペーパーの直径は 12cm 以下、芯の直径は 38mm±1mm なのでここでは 4cm にしています。
半径なので半分です。
R を計算してみましょう。
$$ R=\sqrt{2r^2 – d^2} $$
$$ R=\sqrt{2 \times 6^2 – 2^2} $$
$$ R=\sqrt{2 \times 36 – 4} $$
$$ R=\sqrt{72 – 4} $$
$$ R=\sqrt{68} $$
$$ ∴ R≒8.25 $$
さて、これは半径なので直径は2倍します。
$$ 8.25 \times 2=16.5 $$
ということで2倍巻きの直径は 16.5cm になりました✌
2倍巻きとふつうサイズの比率
直径の比率は、
16.5 ÷ 12 ≒ 1.38
これは芯なしの√2 (1.41) とほとんど変わりません。
芯があるかないかはあまり関係ないということです。
比較のためにあえて 1.41と、小数点以下2桁まで書きました。
小数点以下1桁で四捨五入すれば両方とも 1.4 です😮
どういうことなんでしょうか?
上の式で
2r2 は 72
d2 は 4
72 ≫ 4 です。
4 に比べて、72 のほうがはるかに大きい。
72 から 4 を引いても、68 でほとんど変わりません。
つまり、芯の面積 d2 の 4 は大勢に影響がないということです。
体重 200kg の力士に、5kg の😺ネコが体当りしても微動だにしないということです😄
だから比率の値も
芯なし:1.41
芯あり:1.38
と、ほとんど変わらないのです。
これは近似式でよくつかわれる考えかたで、小数点以下1桁 (この場合、有効数字2桁) ならおなじ 1.4 になってしまうようなときは、d2 のような小さな値は無視してもかまわないのです。
買うのやめた
ふつうサイズの 12cm に対して、4.5cm も大きいです。
これではホルダーに収まりません。
それなのに直径はほとんど変わらないというのはどう考えてもおかしいですね。
おじさんは2倍巻きを買うのをやめました。
6倍巻きまであるそうですが論外です😄
ふつうの1リットルの牛乳パックに6リットルはいると思いますか?🥛