目次をご覧になりたい方はクリックしてください→
「ドーナツ」「面積」「ピタゴラスの定理」

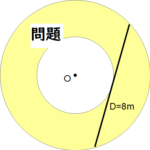
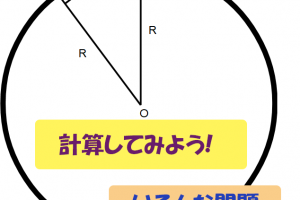
ドーナツ状の面積を求める ~ ピタゴラスの定理 (問題)
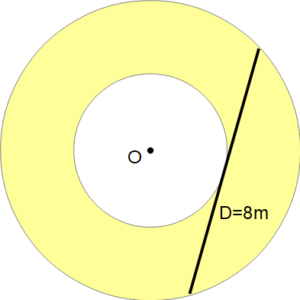
さて、こんな訳のわからない測りかたをしてきたさっちゃんですが、クマはこれでわかるかも!と言いました🐻
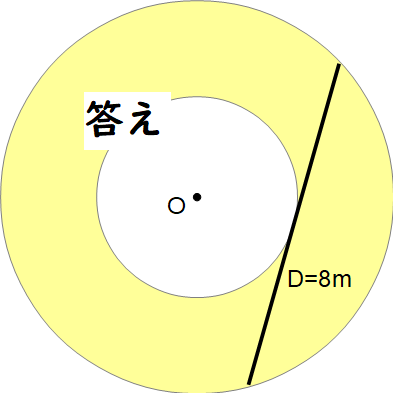
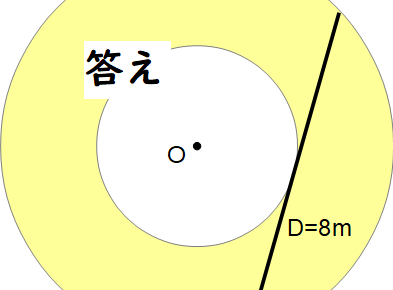
答え
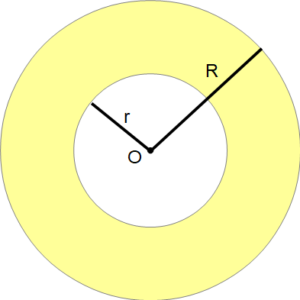
ふつうはこのように
外円 (大円) の面積から内円 (小円) の面積を引けばドーナツ状の床の面積が出ます。
面積:S
外円の半径:R
内円の半径:r
円周率:π
S = πR2-πr2
S = π(R2-r2)
上の絵とこの絵を合体させます。
そして時計の針のように線を動かすとこうなります。
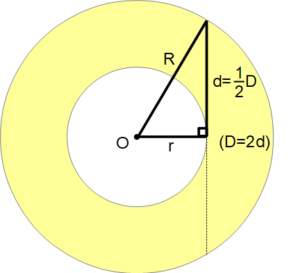

直角三角形が出現😮
接線は円の中心に対して垂直 (直角) です。
そして接点の上下はおなじ長さなので d は D の半分になります。
分数がついてると計算がめんどうなので d をつかいます。
$$ d=\frac{1}{2}D $$
ピタゴラスの定理
d2+r2=R2
d2=R2-r2
これを上の式に代入するとこうなります。
S = πd2
つまり接線 D の半分の d が半径である円の面積になります。
言いかたを変えれば、接線 D が直径である円の面積にほかなりません。

👇 おなじ

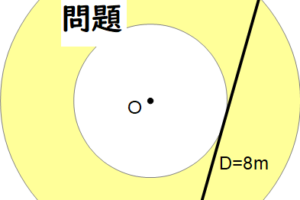
穴の大きさ (小円) や外円の大きさは関係ない
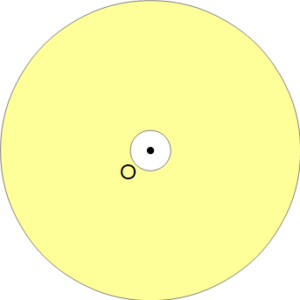

だから穴がなくても、穴が小さくても、大きくても
接線の長さがおなじなら、その直径の円の面積に等しくなります。
ここで8mにしたのはとくに理由はありません😄
代数だけだと拒否反応が起きると思って具体的な数字を入れましたが、大事なことは長さではなく接線の長さがおなじだと面積がおなじということです。
いちおう書いておくと
3.14 × 4 × 4 ≒ 50 [m2] です。
みなさんはわかりましたか?
わかった?
そりゃすごい!