目次をご覧になりたい方はクリックしてください→
「文章問題」「速さ」「近づく」「時間」
接近する場合
お弁当をとどけるお母さん。その2
よくある算数の文章問題です。
『トシくんはいつものとおり家を出て学校に向かいます。
10分後にお弁当を忘れてることに気がつきました!
トシくんは家にもどることにします。
と同時にお母さんも気がついて自転車で弁当を持っていくことにしました。
2人は何分後に出会うでしょうか?
トシくんの歩く速さは1分間に100mです。
お母さんの自転車の速さは1分間に500mとします。』
う~ん。むずかしい問題ですね。
絵を書く
何はさておき、まず「絵」を書きましょう!
わからないところは代数で
数学では x や y を使うけど、それだけでむずかしく感じてしまいます。
ここでは、□ や △ の記号をつかってみましょう。
🐰や🐢や🌟でも何でもいいんですよ。
ただ、あまり複雑な絵だと書くのが大変なのでカンタンな絵にしましょう(^^)
とにかくわかっていることを書き出す
はじめから問題を解こうとしないで、まずわかっていることを洗いざらい書き出します。
数字がわからないところは記号 (代数) で書きます。
わかっていること
トシくんの速さ:100 [ m/分 ]
お母さんの自転車の速さ:500 [ m/分 ]
トシくんが弁当を忘れたことに気がついたのは、家を出てから「10分後」
2人は同時に相手に向かって歩き (こぎ) はじめます。
トシくんがもどりはじめ、同時にお母さんが自転車をこぎはじめてから、2人が出会うまでの時間を「□ [ 分 ]」とします。
家から2人が出会った場所までの距離を「△ [ m ] 」としましょう。
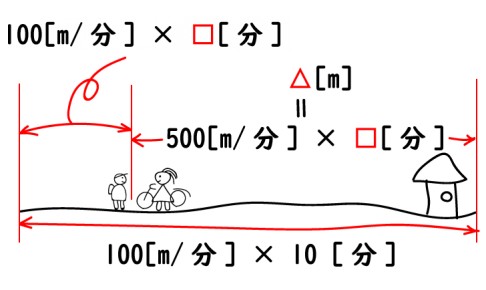
これを絵にします
絵にしながら、わかるところを式にします。
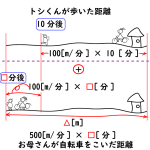
10分後。弁当を忘れたことに気づく!
まずトシくんが歩いた距離を計算しましょう。

距離は速さ × 時間
100 [ m/分 ] × 10 [ 分 ] = 1000 [ m ]
これが、トシくんが「10分間」で歩いた距離です。
2人は同時に歩き (こぎ) だす

めでたく2人は出会う☺
□ [ 分 ] 後、2人は「どこかで」出会います。
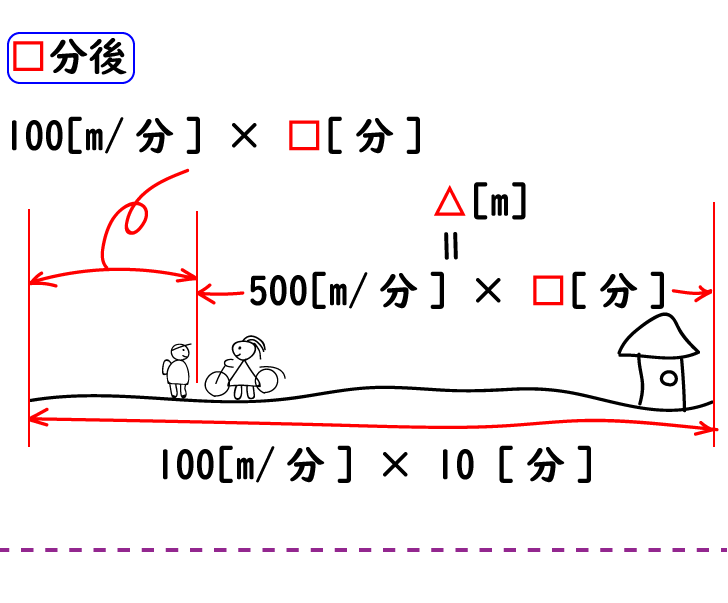
2人が歩いた (こいだ) 距離は合わせて1000 [ m ] !
どこで会ったかは関係ありません!
これを式にしましょう。
トシくんがもどった距離
100 [ m/分 ] × □ [ 分 ]
お母さんが自転車をこいだ距離
500 [ m/分 ] × □ [ 分 ]
なので
100 [ m/分 ] × □ [ 分 ] + 500 [ m/分 ] × □ [ 分 ] = 1000 [ m ]
100 □ + 500 □ = 1000
600 □ = 1000
□ = 1000 ÷ 600
$$ □ = 1 \frac{2}{3}[ 分 ]$$
つまり、1分40秒でした!
歩いた距離は関係ない
上で △ [ m ] とわざわざ書いたけど、じつは距離は関係ありませんでしたね。
2人が出会うのは、家からどれくらいの距離だったかは関係なかったんです。
言いかたを変えれば、この問題は「何分後か? 」なので距離はわからなくてもいいんです。
ただし、最初から時間だけで考えようとするとむずかしいです。
絵を書いて視覚的に距離や位置関係や時間による変化などが見えたほうがわかりやすいです。
もちろん時間がわかったので距離も計算することはできます。
せっかくだから距離も計算してみましょう。
2人が出会うのは家から何m?
△ [ m ] = 500 [ m/分 ] × □ [ 分 ]
$$△ = 500 × 1 \frac{2}{3}$$
$$△ = 500 × \frac{5}{3}$$
$$△ = \frac{2500}{3}$$
△ ≒ 833 [ m ]
ちなみにトシくんがもどった距離は
1000 – 833≒167 [ m ]
でした。


文章問題 ~ お弁当をとどけるお母さん。その1
計算問題 ~ 一覧。みのまわりの算数・数学
たのしい算数・みのまわりの数学 ~ 一覧