目次をご覧になりたい方はクリックしてください→
「速さ」「時速」「公式」「おぼえかた」
算数の公式で最初につまづくのが「面積」や「体積」。
そのつぎが「速さ」ではないでしょうか。
単位が答え!
単位を見れば答え (計算のしかた) がわかります!
速さ
こんな問題がよくあります。
問題 1.
さっちゃんの家からおばあちゃんの家まで80 [ km ] あります。
車で 2 [ 時間 (h) ] かかりました。
車の速さ (時速) をもとめなさい。
答え____[ km/h ]



答えを書くところに [ km/h ] と書いてあるではないですか!
$$ [ km/h ] = [ km ] ÷ [ h ] = \frac{[ km ] }{[ h ] } です。$$
先生は親切にも「『距離』を『時間』で割りなさい」と教えてくれています(^^)
ちなみに、風速は [ m/s ] (秒速何メートル) で表すのがふつうです。
距離
問題 2.
60 [ km/h ] で、3時間 ( [ h ] ) 走りました。
何 [ km ] 走ったか計算しなさい。
答え____[ km ]
$$\frac{ [ km ] }{[ h ] } と [ h ] だから、$$
かける ( × ) と [ h ] が消えて、 [ km ] が残るということがわかりますね!
時間
時間はちょっとややこしいです。
問題 3.
さっちゃんの家からおばあちゃんの家まで60 [ km ] あります。
時速 20キロ ( 20 [ km/h ] ) で走ると、何時間 ( [ h ] ) かかるでしょう?
答え____[ h (時間) ]
わかっているのは
$$ [ km ] と [ km/h ] ( = \frac{ [ km ] }{[ h ] } ) $$
どっちかをどっちかで割れば
$$\frac{ [ km ] }{[ km ] } で、$$
[ km ] が消えてくれることがわかります。問題はどっちをどっちで割ればいいか?
$$\frac{ [ km ] }{[ h ] } を見ると$$
分母に [ h ] がいるので、これを上に出したいですね。
「 ÷ 」×「 ÷ 」 = 「 × 」になるので、
$$\frac{ [ km ] }{[ h ] } を$$
分母 (割る数) に持っていってみましょう。
$$\frac{ [ km ] }{\frac{ [ km ] }{[ h ] }} $$
$$= [ km ] ÷ \frac{ [ km ] }{[ h ] }$$
$$= [ km ] × \frac{[ h ] }{ [ km ] } = [ h ] $$
$$\frac{ [ km ] }{[ km ] } は消えて、$$
みごと [ h ] が上におどり出ました!
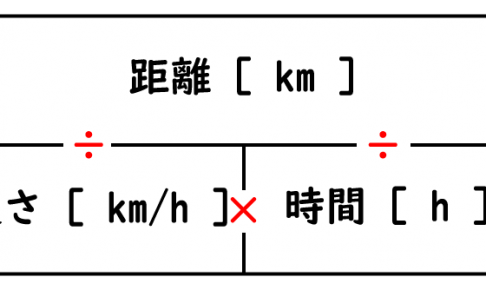
距離・時間・速さ ~ 虎の巻
これらをまとめたのが下の表
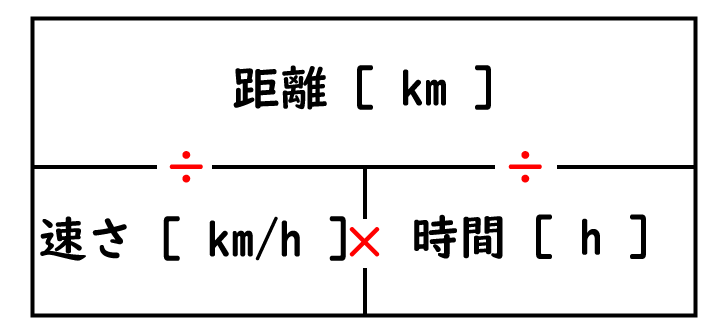
距離はいつでも分子。
距離に対して速さと、時間は分母になる。
つまり「 ÷ (割る) 」ということ。
「距離」÷「時間」=「速さ」
「距離」÷「速さ」=「時間」
速さと時間は「 × (かける) 」ということ。
「速さ」×「時間」=「距離」
この表が覚えられないって?
そのときはいつでも車のスピードメーターを思い出して!
$$ [ km/h ] = [ km ] ÷ [ h ] = \frac{[ km ] }{[ h ] } です。$$
これさえ見れば、
「距離」÷「時間」=「速さ」
ということがわかります。
あとは移項すれば他の計算もできます。
密度 [ g/cm3 ] の計算 ~ 虎の巻
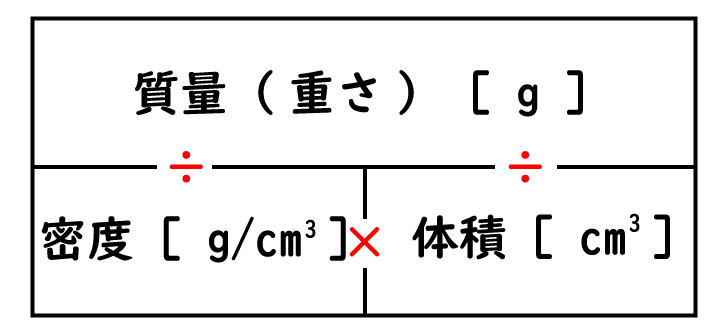
密度の計算も速さとおなじ表がつかえます!
重さはいつでも分子。
重さに対して密度と、体積は分母になる。
つまり「 ÷ (割る) 」ということ。
「重さ」÷「体積」=「密度」
「重さ」÷「密度」=「体積」
密度と体積は「 × (かける) 」ということ。
「密度」×「体積」=「重さ」
この表が覚えられないって?
単位は [ g/cm3 ] です。
これさえ覚えとけば、
「重さ」÷「体積」=「密度」
ということがわかります。
あとは移項すれば他の計算もできます。

単位と次元 ~ 時速の計算についてはこちら
時速と秒速の換算はこちら
たのしい算数・みのまわりの数学 ~ 一覧

おじさんオススメの記事
注目の記事
話題の記事
人気の記事