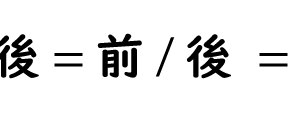目次をご覧になりたい方はクリックしてください→
「単位」「次元」「面積」「体積」「速さ」
単位
「助数詞」は「単位」ではない
日本語にはちょっと厄介な問題があります。
それは「1個」「2本」「3枚」のように、数字の後ろにくっつく言葉があることです。
これは数学上は「単位」ではありません!
「助数詞」と呼ばれます。
英語ではただ「1 (ワン) 」「2 (トゥー) 」「3 (スリー) 」のように数えて後ろには何もつきません。
助数詞なのか、単位なのか? 見分けかた
助数詞の場合は後ろの
「個」「本」「枚」のような言葉を取ってしまっても意味が変わりません。
言いかたを変えると、
「ひとつ」「ふたつ」「みっつ」または「1」「2」「3」と数えられれば「助数詞」です。
ほかに「台」「件」「人」「頭」「冊」などがあります。
みなさんも探してみてください。
基数詞 (きすうし)
「ひとつ」「ふたつ」「みっつ」のように何もつけないで数えられる数字そのものは「基数詞」といいます。
助数詞 (じょすうし)
その後ろにつける「個」「本」「枚」などで、単位ではありません。
これらはつけなくても数えられます。
序数詞 (じょすうし)
「1番目」「2番目」「3番目」
英語ならfirst, second, thirdのように「順番」「順序」を表す数字を序数詞と言います。
読みかたは、助数詞とまったくおなじなので非常に紛らわしいのですが、似て非なるものです。
無次元数 (むじげんすう)
数学では、このように単位のない数を
「無次元数」
といいます。
おぼえなくていいよ(^^)
単位は?
単位の場合は
[ km (キロメートル) ] [ h (時間) ] [ kg (キログラム) ] [ ml (ミリリットル) ]などのように取ってしまうと、
距離なのか、時間なのか、重さなのか、体積なのか、わからなくなってしまいます。
次元
- 0次元。点
- 1次元。長さだけ
- 2次元。面積
- 3次元。体積
0 次元
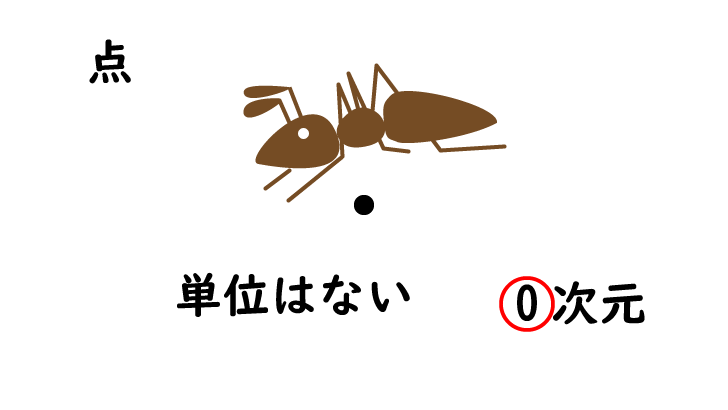
0 次元アリは、
点から動くことができません。
1 次元
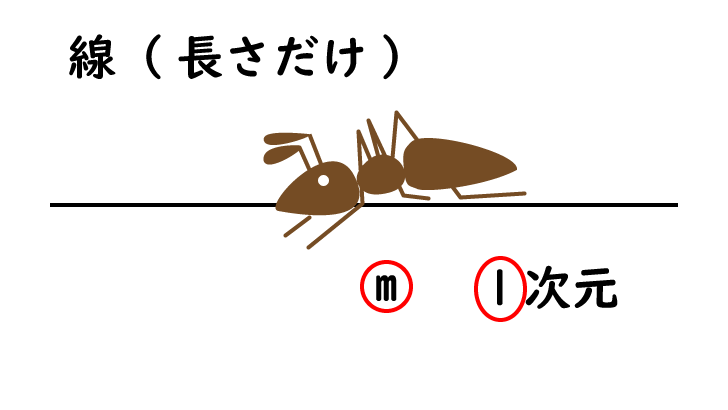
1 次元アリは、
線の上だけ行き来できます。
長さだけなので、単位は[ m ]
1 乗の場合は肩に何もつけないけど
そこに「 1 」が隠れていると思ってください。
2 次元
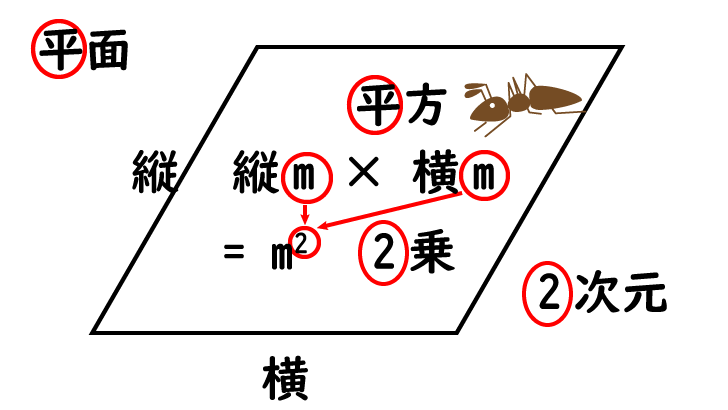
2 次元アリは、
平面 (縦、横) だけ歩けます。
上や下には行けません。
地面を這いずり回ってるわたしたち人間みたいなものです(^_^;)
縦と横の 2方向の長さがあるので、
単位は m × m = [ m2 ]
右肩についてる小さい 2 は、
m を「2 回かけた」
または「2 コかけた」という意味です。
2次元コンプレックス
マンガやアニメなどのキャラクターにしか好きになれない人を
「2次元コンプレックス」なんていいますね=^^=
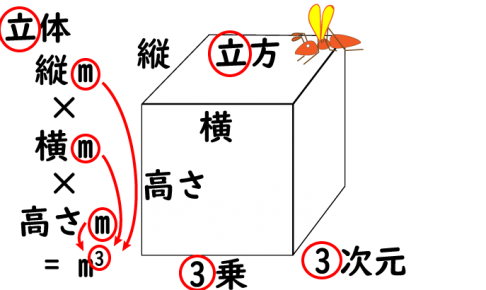
3次元
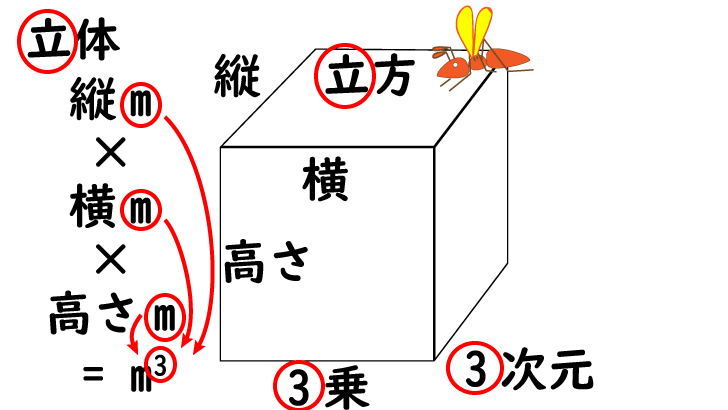
3 次元アリは、
立体 (縦、横、高さ) の中を自由に動けます。
空を飛ぶ鳥のようですね。
あっ! いつの間にか羽が生えてます!
縦、横、高さの 3方向の長さがあるので、
単位は m × m × m = [ m3 ]
右肩についてる小さい 3 は、
m を「3 回かけた」
または「3 コかけた」という意味です。
3D (スリー・ディー)
3-dimension(-al)
3次元のことです。
平面なのに立体的に見える映像などをいいます。
飲みものに書いてある単位
cc は
「cubic centi-meter (立体的 センチメートル) 」の略です。
数学では
[ cm3 (立方センチメートル) ] と書きます。
ml は
「milli-liter (ミリ リットル。つまり、1/1000 リットル) 」の略です。
体積としては、1 cc = 1 cm3 = 1 ml です。
1辺 1cmのサイコロがこの大きさです。
ちなみに1 cc の水が、1 g です。
面積、体積の公式
よくある円や球の面積や体積。
おぼえるのが大変ですね。
円
円周
$$2πr$$
円の面積
$$πr^2$$
球
球の表面積
$$4πr^2$$
おぼえかた「心配ある事情」
球の体積
$$\frac{4πr^3}{3}$$
おぼえかた「身の上に心配ある参上」
迷ったら肩の数字を見る!
肩の数字が「1」なら「長さ」
肩の数字が「2」なら「面積」
肩の数字が「3」なら「体積」


💡 何乗してるかがヒント!
「 r 」1乗なら長さ (肩には何もつきません)
「 r2 」2乗なら面積
「 r3 」3乗なら体積
円と球の公式。
それぞれ面積と体積の式が似ているのには理由があります。
面積を積分すると、体積。
体積を微分すると、面積になります。
ここでは、おぼえなくていいです(^^)
高校生の人は「なるほど! 」と思いますね=^^=
単位が答え!
単位を見れば答え (計算のしかた) がわかります!
速さ
こんな問題がよくあります。
問題 1.
さっちゃんの家からおばあちゃんの家まで80 [ km ] あります。
車で 2 [ 時間 (h) ] かかりました。
車の速さ (時速) をもとめなさい。
答え____[ km/h ]



答えを書くところに
[ km/h ]と書いてあるではないですか!
$$ [ km/h ] = [ km ] ÷ [ h ] = \frac{[ km ] }{[ h ] } です。$$
先生は親切にも
「『距離』を『時間』で割りなさい」
と教えてくれています(^^)
ちなみに、
風速は [ m/s ] (秒速何メートル) で表すのがふつうです。
速度の記号についてはこちら。「:」比 =「÷」割り算 =「/」「ー」分数なのだ!
時速 (速さ) の計算 ~ おぼえかたにつづく!
体積 [ m3 ]
問題 4.
縦 4m、横 2m、高さ 3m の箱があります。
体積をもとめなさい。
答え____m3


密度 [ g/cm3 ]
これも、
重さ [ g ] / 体積 [ cm3 ] = 密度 [ g/cm3 ]
って教えてくれてますね。
重さ ÷ 体積なので、[ kg/m3 ] という単位もあります。
速度の計算とまったく同じです。
距離 [ km ] / 時間 [ h ] = 速さ [ km/h ]
あとは「移項」すれば、それぞれの値がもとめられます。
たのしい算数・みのまわりの数学 ~ 一覧はこちら